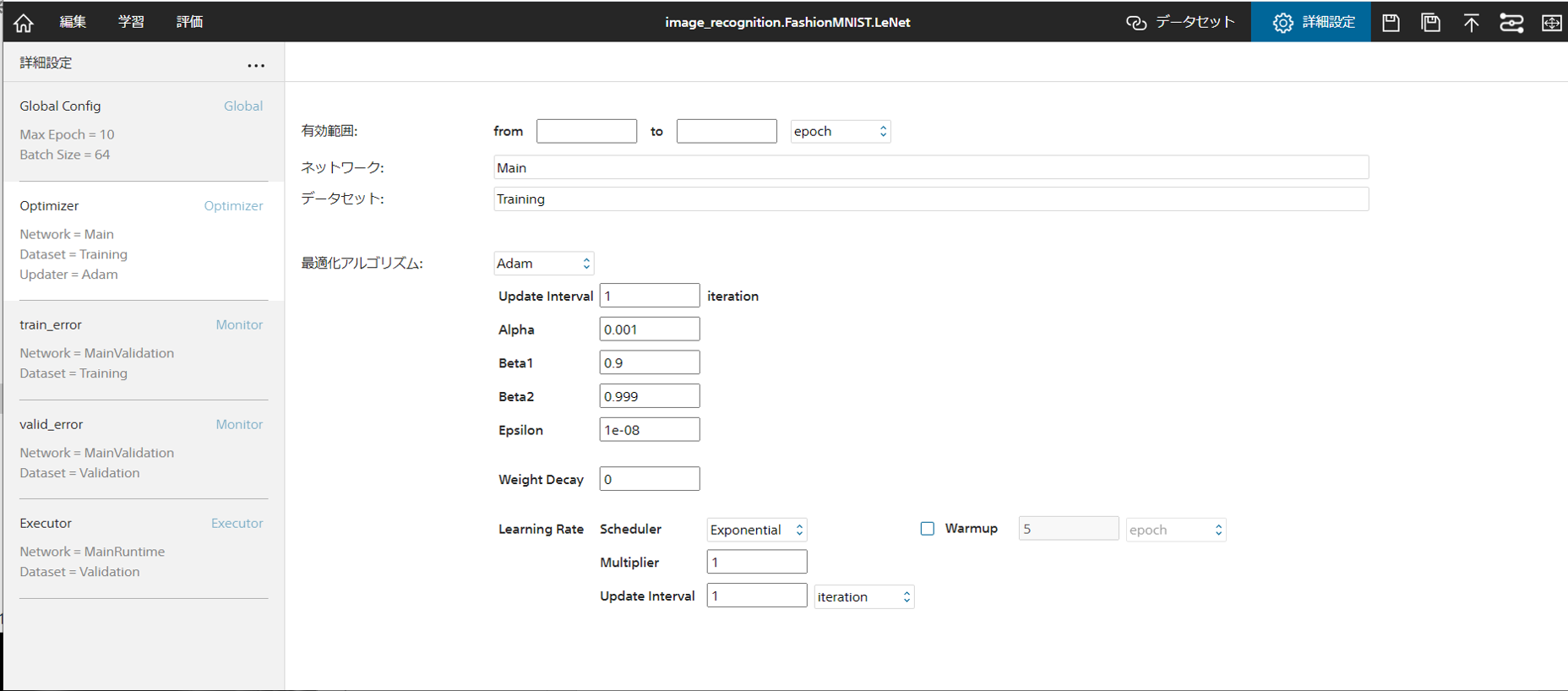
1 Optimizerを有効にする範囲を指定するには
有効範囲のfrom、toにそれぞれ有効にする範囲iterationもしくはepoch単位で指定します。
例えば、Optimizerを50 epoch~100 epochまで有効にするには、fromに50、toに100を入力します。1 epoch~Max Epochまで全ての範囲でOptimizerを有効にするには、from、toいずれも空欄にします。
2 最適化に用いるネットワークの名前を指定するには
ネットワークに編集タブで作成したネットワーク名を指定します。
3 最適化に用いるデータセットの名前を指定するには
データセットにデータセットタブで読み込んだデータセット名を指定します。Optimizerで複数のデータセットを同時に用いる場合は、複数のデータセットの名前をカンマ区切りで指定します。
4 パラメータのアップデート手法を指定するには
- コンフィグリストから最適化アルゴリズムを選択します。
- 最適化アルゴリズムを以下から選択します(デフォルトはAdam)。
AdaBound
$$wt+1 ← wt – ηt ∗ mt\
\eta t=clip\left(\alpha\frac{\sqrt{1-\beta_2^t}}{\left(1-\beta_1^t\right)\left(\sqrt{v_t}+\varepsilon\right)},\eta l\left(t\right),\eta u\left(t\right)\right)\
ηl(t)=(1−(1/((1−β)t+1)))α\
ηu(t)=(1+(1/((1−β)t)))α$$
L. Luo, Y. Xiong, Y. Liu and X. Sun.
Adaptive Gradient Methods with Dynamic Bound of Learning Rate.
https://arxiv.org/abs/1902.09843
AMSBound
$$wt+1 ← wt – ηt ∗ mt\
\eta t=clip\left(\alpha\frac{\sqrt{1-\beta_2^t}}{\left(1-\beta_1^t\right)\left(\sqrt{{\hat{v}}t}+\varepsilon\right)},\eta l\left(t\right),\eta u(t)\right)\
{\hat{v}}_t=max\left({\hat{v}}{t-1},\ v_t\right)\
ηl(t)=(1−(1/((1−β)t+1)))α\
ηu(t)=(1+(1/((1−β)t)))α$$
L. Luo, Y. Xiong, Y. Liu and X. Sun.
Adaptive Gradient Methods with Dynamic Bound of Learning Rate.
https://arxiv.org/abs/1902.09843
| Updater | 更新式 |
| Adadelta |
$$g_t \leftarrow \Delta w_t\\ Matthew D. Zeiler ADADELTA: An Adaptive Learning Rate Method |
| Adagrad | $$g_t \leftarrow \Delta w_t\\ G_t \leftarrow G_{t-1} + g_t^2\\ w_{t+1} \leftarrow w_t – \frac{\eta}{\sqrt{G_t} + \epsilon} g_t$$John Duchi, Elad Hazan and Yoram SingerAdaptive Subgradient Methods for Online Learning and Stochastic Optimizationhttp://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf |
| Adam | $$m_t \leftarrow \beta_1 m_{t-1} + (1 – \beta_1) g_t\\ v_t \leftarrow \beta_2 v_{t-1} + (1 – \beta_2) g_t^2\\ w_{t+1} \leftarrow w_t – \alpha \frac{\sqrt{1 – \beta_2^t}}{1 – \beta_1^t} \frac{m_t}{\sqrt{v_t} + \epsilon}$$Kingma and BaAdam: A Method for Stochastic Optimization.https://arxiv.org/abs/1412.6980 |
| Adamax | $$m_t \leftarrow \beta_1 m_{t-1} + (1 – \beta_1) g_t\\ v_t \leftarrow \max\left(\beta_2 v_{t-1}, |g_t|\right)\\ w_{t+1} \leftarrow w_t – \alpha \frac{\sqrt{1 – \beta_2^t}}{1 – \beta_1^t} \frac{m_t}{v_t + \epsilon}$$Kingma and BaAdam: A Method for Stochastic Optimization.https://arxiv.org/abs/1412.6980 |
| AMSGRAD | $$m_t=\beta_1m_{t-1}+\left(1-\beta_1\right)g_t\\ v_t=\beta_2v_{t-1}+\left(1-\beta_2\right){g_t}^2\\ {\hat{v}}_t=max\left({\hat{v}}_{t-1},\ v_t\right)\\ \theta_{t+1}=\theta_t-\alpha\frac{m_t}{\sqrt{{\hat{v}}_t}+\varepsilon}$$Reddi et al.On the convergence of ADAM and beyond.https://openreview.net/pdf?id=ryQu7f-RZ |
| Momentum | $$v_t \leftarrow \gamma v_{t-1} + \eta \Delta w_t\\ w_{t+1} \leftarrow w_t – v_t$$Ning QianOn the momentum term in gradient descent learning algorithmshttp://www.columbia.edu/~nq6/publications/momentum.pdf |
| Nag | $$v_t \leftarrow \gamma v_{t-1} – \eta \Delta w_t\\ w_{t+1} \leftarrow w_t – \gamma v_{t-1} + \left(1 + \gamma \right) v_t$$Yurii NesterovA method for unconstrained convex minimization problem with the rate of convergence o(1/k2) |
| RMSprop | $$g_t \leftarrow \Delta w_t\\ v_t \leftarrow \gamma v_{t-1} + \left(1 – \gamma \right) g_t^2\\ w_{t+1} \leftarrow w_t – \eta \frac{g_t}{\sqrt{v_t} + \epsilon}$$Geoff HintonLecture 6a : Overview of mini-batch gradient descenthttp://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf |
| Sgd | $$w_{t+1} \leftarrow w_t – \eta \Delta w_t$$ |
θ:更新対象のパラメータ
g:勾配
η、α:Learning Rate、Alpha(学習係数)
γ、β1、β2:MomentamもしくはDecay、Beta1、Beta2(Decayパラメータ)
ε:Epsilon(ゼロ除算を防ぐために用いる小さな値)
5 Weight Decay(L2正則化)の強度を設定するには
Weight DecayにWeight Decayの係数を指定します。
6 学習係数の減衰方法を指定するには
- コンフィグリストからOptimizerを選択します。
- 最適化アルゴリズムのLR Scheduler (Learning Rate Scheduler)を以下から選択します(デフォルトはExponential)。
- Linear Warmupを行う場合、Warmupをチェックし、Warmupの長さをiterationもしくはepochで指定します。
Polynomial
学習係数を以下の多項式で減衰します。
$$\eta_t=\eta_0\left(1-\left(\frac{t}{T}\right)^p\right)$$
Powerにpに用いる係数を指定します。
t:現在までのパラメータ更新回数
ηt :パラメータ更新に用いる学習係数
η0 :Updaterで指定する学習係数
T : 学習終了までのパラメータ更新回数
Step
学習係数を指定するiterationもしくはepoch毎に指定倍に減衰します。
Learning Rate Multiplierに学習係数を減衰させる係数を、LR Update Stepsに学習係数を減衰させるタイミングをカンマ区切りの数値で指定します。
例えば学習係数を20万、30万、40万iterationで0.1倍に減衰させるには、Learning Rate Multiplierを0.1、LR Update Stepsに「200000,300000,400000」 iterationとします。
例えば学習係数を30、60、80 epochで0.1倍に減衰させるには、Learning Rate Multiplierを0.1、LR Update Stepsに「30,60,80」epochとします。
| LR Scheduler | 解説 |
| Cosine | 以下の式に従い学習係数を減衰します。 $$\eta_t=\frac{\eta_0}{2}\left(1+cos\left(\frac{t}{T}\pi\right)\right)$$t:現在までのパラメータ更新回数 ηt :パラメータ更新に用いる学習係数 η0 :Updaterで指定する学習係数 T : 学習終了までのパラメータ更新回数 |
| Exponential | 学習係数を指数関数で減衰します。Learning Rate Multiplierに学習係数を減衰させる係数を、LR Update Intervalに学習係数を減衰させる間隔を指定します。 例えば学習係数をMini-batch毎に0.9999倍に減衰させるには、Learning Rate Multiplierを0.9999、LR Update Intervalを1 iterationとします。学習係数を20 epoch毎に0.1倍に減衰させるには、Learning Rate Multiplierを0.1、LR Update Intervalを1 epochとします。 |
7 パラメータの更新を複数回のMini-batchに1回行うには
Update Intervalにパラメータの更新を行う間隔を指定します。例えば64個のデータを含んだMini-batchを用いて4回勾配を計算し、4回のMini-batchごとにまとめてこれらの勾配を用いたパラメータの更新を行うには、Batch Sizeを64、Update Intervalを4とします。
ご注意
複数の学習用ネットワークを用いた最適化を行う場合、Update Intervalには常に1を指定する必要があります。
8 新しいOptimizerを追加するには
メニューボタン、もしくはコンフィグリストを右クリックして表示されるポップアップメニューから「Optimizerを追加」を選択します。
9 Optimizerの名前を変更するには
- メニューボタン、もしくはコンフィグリストを右クリックして表示されるポップアップメニューから「名前変更」を選択します。
- もしくはコンフィグリストから、名前を変更するOptimizerを2度クリックします。
- 新しい名前を入力してキーボードのEnterキーを押します。
10 Optimizerを削除するには
- コンフィグリストで、削除するOptimizerを選択します。
- メニューボタン、もしくはコンフィグリストを右クリックして表示されるポップアップメニューから「削除」を選択します。
- もしくは、キーボードのDeleteキーを押します。
11 Optimizerを並び替えるには(NNabla)
- コンフィグリストで、並び替えるOptimizerを選択します。
- メニューボタン、もしくはコンフィグストを右クリックして表示されるポップアップメニューから「上に移動」もしくは「下に移動」を選択します。
