本チュートリアルでは、入力画像を元に何らかの連続値を算出するニューラルネットワークの学習方法について解説します。以下に画像を元に連続値を出力するニューラルネットワークのイメージを示します。
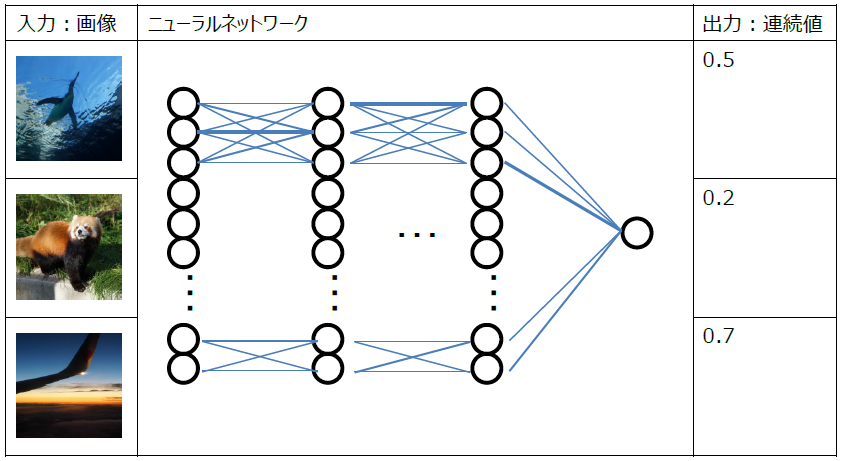
入力画像から連続値を出力するニューラルネットワークのイメージ
入力データxから連続値yを求めるような関数y=f(x)を推定する問題を、機械学習、統計学の分野では「回帰」と呼びます。
例えばこのニューラルネットワークは、画像のクオリティーを表す点数の推定、画像のノイズ量、シャッタースピードなどの推定、画像加工に利用する明るさ、コントラスト、ガンマなどのパラメータの推定、画像に含まれる物体の数、大きさ、座標の推定など様々なシーンで活用することができます。
データセット
ここでは解説の題材として、Neural Network Consoleにおいてデフォルトで利用可能なMNISTデータセットを用います。MNISTデータセットは60,000枚の学習用画像と10,000枚の評価用画像を含みます。各画像は28×28ピクセルのモノクロ画像であり、各画像について正解の数字のIndex(0~9)が与えられています。
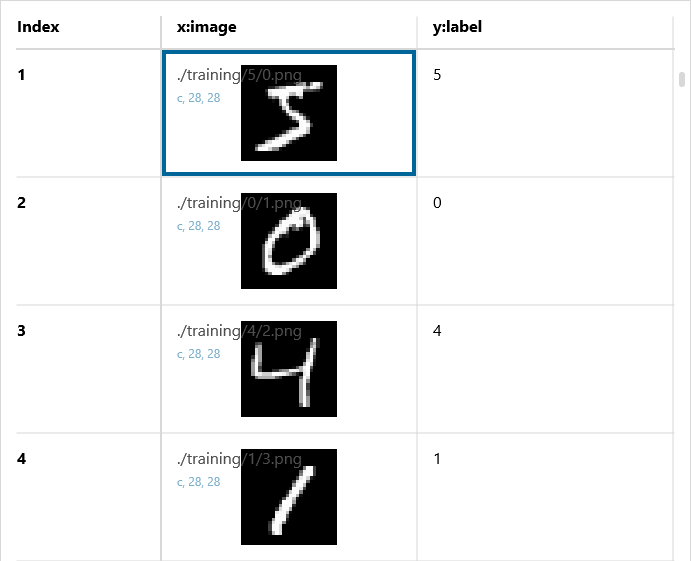
MNISTデータセット
本来このデータセットは0~9の数字を0~9の10のカテゴリに分類するためのものですが、今回はこれを画像から0.0~9.0の連続値ラベルを推定するためのデータセットとして利用します。自力でデータセットを用意する際も、このように画像xに対して正解の値yを与えるようなデータセットを用意することで、連続値を推定するニューラルネットワークを学習させることができます。
ネットワーク構造
連続値を推定する場合に用いるネットワーク構造は、カテゴリ分類のためのネットワーク構造とほとんど同じです。今回は以下のようなネットワーク構造を用います。
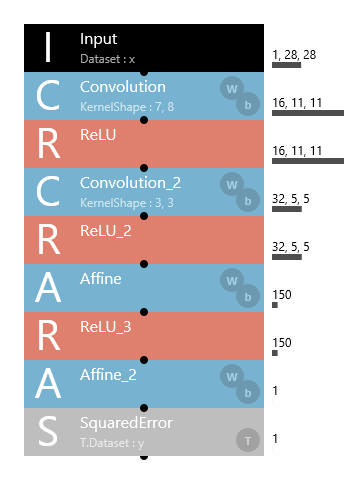
画像から連続値を推定するニューラルネットワーク構造
1x28x28の画像を入力し、1つの連続値を推定するようなネットワーク構造になっています。2回のConvolutionではStrideを2,2とすることで、MaxPooling等を使わずに画像の解像度を1/2にダウンサンプリングしています。
カテゴリ分類のためのネットワーク構造(Neural Network Console同梱の多くのサンプルプロジェクトがこれにあたる)との差分はネットワークの最後にあります。具体的にはカテゴリ分類問題ではSoftmax+CategoricalCrossEntropy、もしくはSotmaxCrossEntropyで終わっていたのに対し、上記ネットワーク構造では末端にSquaredErrorを用いています。
カテゴリ分類問題におけるSoftmax+CategoricalCrossEntropy、もしくはSotmaxCrossEntropyは、ニューラルネットワークの出力値を全カテゴリで足して1になるような0.0~1.0の確率に正規化し(Softmax)、こうして得られた確率が与えられたラベルと一致するほど出力値が小さくなるロス関数(CategoricalCrossEntropy)を用いてニューラルネットワークのパラメータを最適化するためのものでした。これに対して連続値推定問題では、ニューラルネットワークの出力値と連続値で与えられたラベルとの平均二乗誤差を表すロス関数であるSquaredErrorを用いてニューラルネットワークを最適化します。
このようなネットワーク構造を用いることで、学習が進むにつれニューラルネットワークの出力値がラベルで与えた値に近づくことが期待できます。
学習結果
それでは実際に上記データセットとネットワーク構造を用いた学習を実行してみましょう。今回CPUを用いて30分ほどで学習が完了しました。
以下に学習結果のLearning Curveを示します。Cost、Training Error、Validation Errorの値は、SquaredErrorの出力値(ニューラルネットワークの出力値と正解ラベルとの平均二乗誤差)となっています。
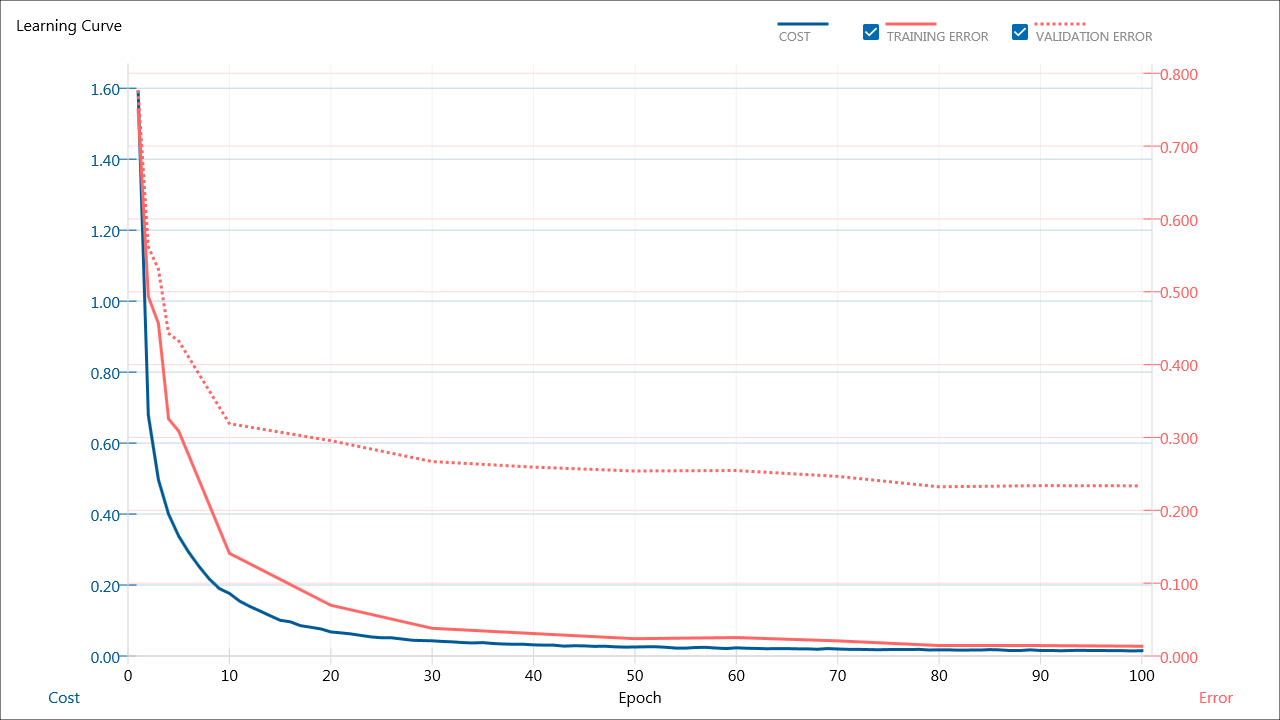
Learning Curve
1 epoch 学習終了時点で0.77だったValidation Errorの値は100 epoch時点では0.23にまで下がっています。学習が進むにつれ、ニューラルネットワークの出力値と正解ラベルとの二乗誤差(y’ – y)^2が小さくなっていることが分かります。
推定結果
以下に学習したニューラルネットワークを用いて、評価用データセットに対して連続値を推定した結果を示します。
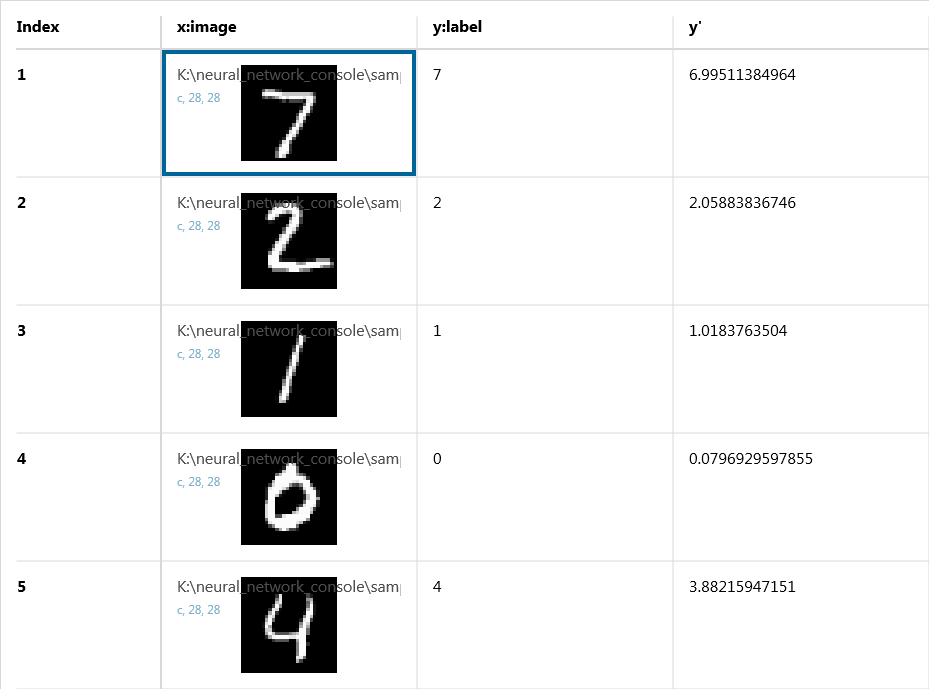
評価結果
推定値として、1つの連続的な値を取るy’が出力されていること、また、推定されたy’はラベルとして与えたyと近い値になっていることが分かります。
連続値の推定結果を他の方法でも確認するため、学習結果の出力フォルダにあるoutput_result.csvをExcelで開いてみましょう(Windows版をご利用の場合)。yとy’の列を選択し、散布図を作成します。
作成した散布図は横軸が正解ラベル(y)、縦軸が画像を元にニューラルネットワークの出力した推定値(y’)となっています。
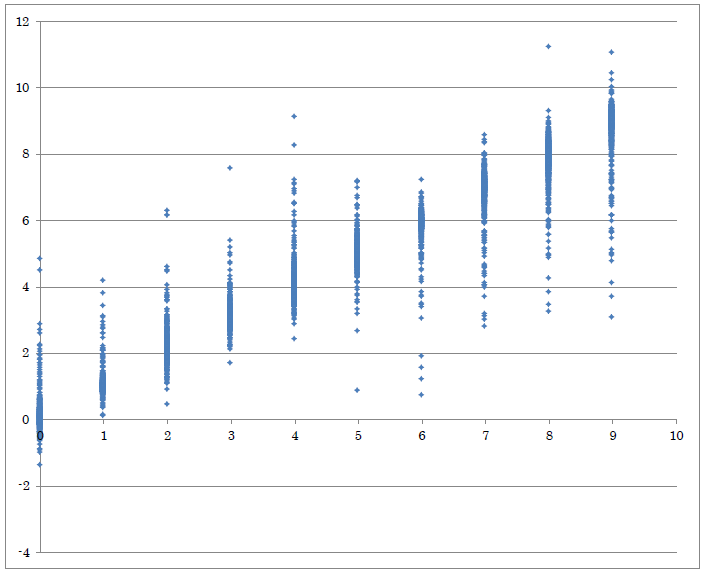
正解ラベル(y:横軸)と推定結果(y’:縦軸)の散布図
0~9いずれの画像についても、出力値(y’)が正解ラベル(y)と近い値になっていることがわかります。
発展形
今回紹介したネットワーク構造は、連続値推定の考え方を紹介するための極めてシンプルなネットワーク構造になっています。最新のテクニックを盛り込んだネットワーク構造を採用することで、同じデータセットを用いながらより高い精度が得られることが期待できます。
回帰問題を扱う場合、ロス関数としてSquaredErrorの代わりにHuberLossを用いることで、より安定した連続値推定が可能なケースがあることが知られています。HuberLossは、二乗誤差が一定以上になると線形にロスが増加するように設計されたロス関数です。
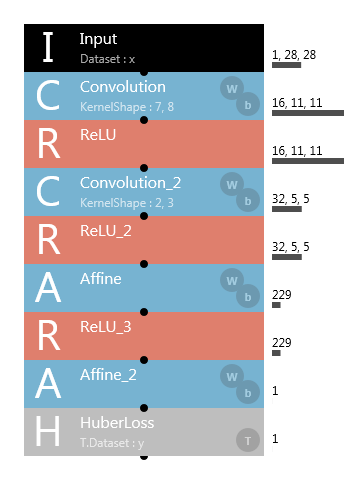
HuberLossを用いたニューラルネットワーク構造
正解ラベルであるyを1次元ではなく、ベクトルとして与えることにより、1つの画像から複数の連続値を同時に推定させることも可能です。例えば4つの連続値を推定させる場合、データセットにおいてy__0~y__3(変数名+ダブルアンダースコア+ベクトルの次元Index)で与えられる4次元の正解ベクトルを与えます。
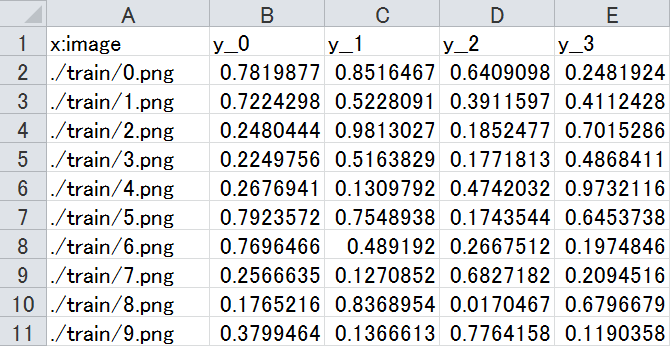
例:4次元の連続値推定のためのデータセット
また、画像入力-画像出力のネットワークを学習することにより、画像全体から1つの連続値を推定させるのではなく、画像の領域、もしくはPixel毎に連続値を推定させることも可能です。
